Planejamento da disciplina

Metodologia

Aula expositiva, exposição de transparências.

A disciplina tem duas lista de exercícios a serem desenvolvidas pelos discentes.

Aula prática de simulações em software OCTAVE, opcional MATLAB.

As aulas expositivas sobre uso do OCTAVE e/ou MATLAB serão gravadas e disponibilizadas no youtube para os alunos.

As atividades acadêmicas serão registradas no SIGAA.

O atendimento ou interação com os estudantes para esclarecimentos de dúvidas ou questões ligadas ao conteúdo da disciplina serão realizadas via hora marcada na sala do professor, via whatsapp ou via video conferência com hora marcada.

Objetivos gerais

Aprofundar os conhecimentos de modelagem matemática de sistemas dinâmicos e introduzir conceitos elementares no projeto de controladores no domínio do tempo.

Objetivos específicos

O aluno deve ser capaz de: (a) Entender a modelagem matemática; (b) Simular um modelo matemático; (c) Projetar controladores no domínio do tempo

Ementa

Modelagem matemática de sistemas dinâmicos através de equações diferenciais e no espaço de estados. Análise de estabilidade de sistemas dinâmicos. Princípios de controle de malha aberta e de malha fechada; projeto de controladores elementares no domínio do tempo.

Conteúdo programático

1. Modelagem matemática de sistemas dinâmicos através de equações diferenciais.

2. Modelos matemáticos de sistemas dinâmicos.

3. Princípios de controle automático: controle de malha aberta e de malha fechada.

4. Análise de estabilidade de sistemas dinâmicos.

5. Análise de resposta transitória e de regime estacionário.

6. Modelagem matemática de sistemas dinâmicos no espaço de estados.

7. Modelagem matemática de sistemas dinâmicos no espaço de estados. Diagramas de blocos.

8. Retroação com variáveis do estado.

Descrição dos instrumentos e critérios de avaliação qualitativa

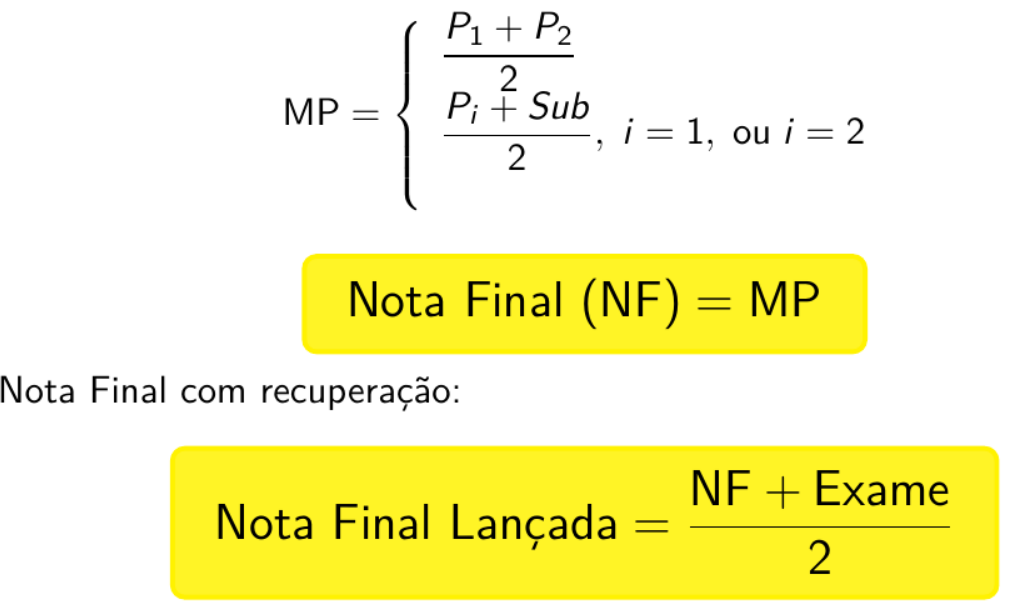
Avaliações relacionadas ao conteúdo teórico das aulas. Nota final será calcula da seguinte maneira:

Primeira Avaliação: P₁

Segunda Avaliação: P₂

Listas:

As listas DEVERÃO SER ENTREGUES NAS RESPECTIVAS DATAS SOLICITADAS (IMPRETERIVELMENTE). Será acrescido de até $0,2$ pontos da Nota Final se e somente se as listas forem entregues totalmente resolvidas nas respectivas datas das avaliações, isto é:
    $NF = NF + 1,0$
   

Seja $n=2$ o número de listas e seja a nota de cada lista denotada por $L_i$ onde $i=1$, $2$. O valor a ser adicionado à Nota Final é determinada da seguinte maneira:
$\left( \dfrac{L_1 + L_2}{2}\right)  \times 0,1.$

Atividades:

Se avaliará semanalmente ou quinzenalmente os conhecimentos dos alunos através de Atividades semanais/quinzenais obrigatórios de serem submetidos nas datas preestabelecidas. As atividade consistiram de pelos menos 2 questões e no máximo 6 questões. O tempo para responder as atividades pode variar entre 30 minutos a 2 horas.
    
Se o discente submeter as atividades semanais nas datas preestabelecidas total e corretamente resolvidas será acrescida à Nota Final uma pontuação de até $1,0$ (um ponto), isto é:
    $NF = NF + 1,0$

Seja $N$ o número de atividades e seja a nota de cada atividade denotada por $Q_i$ onde $i=1$, $2$, $\ldots$, $N$. O valor a ser adicionado à Nota Final é determinada da seguinte maneira:
$\left( \dfrac{Q_1 + Q_2 + \cdots + Q_N}{N}\right)  \times 0,1.$       

* Será acrescido de 0,4 pontos da Nota Final se e somente se o discente entregar as duas listas totalmente resolvidas nas respectivas datas da primeira e segunda avaliação.

Referências bibliográficas básicas

1.     DORF, Richard C.; BISHOP, Robert H. Modern Control Systems. 11.ed. New Jersey: Pearson: Prentice Hall, 2008. 1018 p.

2. OGATA K.; Engenharia de Controle Moderno. 5.ed. São Paulo: Pearson Prentice Hall, 2010. 809 p.

3. ZILL, Dennis G. Equações Diferenciais com Aplicações em Modelagem. São Paulo: Pioneira Thomson Learning, 2003. 492 p.

1.     BASSANEZI, R.C. Ensino-aprendizagem com modelagem matemática. São Paulo: Contexto, 2002.

2. CHIANG, A.; WAINWRIGHT, K. Mathematica para economistas . Rio de Janeiro: Elsevier, 2006.

3. FOWLER, A. C. Mathematical models in the applied sciences. Cambridge: Cambridge, 1997. 402 p. (Cambridge texts in applied mathematics).

4. VACCARO, R. J.; Digital Control. Mcgraw-Hill College, 1995.